¿Qué cosa es el porcentaje?

Es algo que todos hemos escuchado una infinidad de veces, y que todo el mundo, se supone, saben manejar. Justamente por eso, entra dentro de las categorías de cosas en las que a uno/a podría darle vergüenza preguntar de que se trata o pedir ayudar para entender algún detalle.

Peor que no saber algo que es útil, es saber que uno no sabe, y no pedir ayuda para salirse de esa posición de "no saber". Si el ego funcionara mas o menos bien, nos debería preocupar menos lo que otros puedan pensar de nosotros y más la percepción de nuestras propias debilidades o fortalezas para enfrentar la realidad, como por ejemplo, saber o no saber si en el hot sale te están cagando con el supuesto porcentaje de rebaja.

Y para saber eso, se requiere saber dos cosas:

• entender y calcular porcentajes

• entender como algunas empresas manipulan los precios en el tiempo para simular rebajas

Una idea útil

Cuando usamos fracciones, por ejemplo \(\frac{3}{5}\) estamos representando una relación entre dos números, donde el denominador, el que está abajo, hace las veces del "total" y el numerador nos indica cuantas partes de ese total tenemos. En \(\frac{3}{5}\) podemos decir que tenemos $3$ de $5$ (supongamos un objeto que se divide en 5).

Tener \(\frac{2}{4}\) que se simplifica a \(\frac{1}{2}=0,5\) implica que tenemos la mitad de ese total, que en este caso es 4.

Recordemos que podemos tomar el total como "uno" en una fracción, (porque \(\frac{A}{A}=1\) para cualquier cosa que pongamos en lugar de $A$) por lo que tener $0,5$ es justamente la mitad (pero expresado en forma decimal).

A veces, las fracciones son mas complicadas, como \(\frac{13}{57}\), en este caso nos preguntamos ¿como saber que tanto tenemos del total? ¿la mitad? ¿mas de la mitad? ¿una parte mucho menor que la mitad?

Una idea útil es asignar a nuestro total el número $100$ y pensar en las partes de $100$. Uno tiene seguro, una idea un poco mas intuitiva cuando hablamos en "partes de cien": tener diez de cien, veinte de cien, cincuenta de cien, o noventa de cien, dan imágenes claras sobre "que tanto" tenemos en relación al total. Podríamos haber elegido cualquier otro número en vez de $100$, pero creo que todos estamos a cuerdo que es mas conveniente elegir $100$ y no $987$.

Sería bueno poder aplicar esto, a cualquier número, a cualquier fracción, y esto es, justamente lo que hacemos cuando calculamos porcentajes.

Supongamos que tengo 15 de 128, es decir \(\frac{15}{128}\) ¿Cuál sería el equivalente si quisiéramos transformarlo en partes de cien?

Calcular porcentajes

La forma en que acabamos de deducir el sentido de los porcentajes no es la mas directa, o sencilla de aplicar siempre. Veamos un ejemplo

¿Cuanto es el 15% de 12800?, uno podría plantear lo mismo que antes:

Es un poco largo, pero de esta ecuación podemos encontrar dos formas de calcular porcentajes muy rápido y fácil.

Si ven la parte izquierda del anteúltimo paso, la fracción \(\frac{15}{100}\) está representando "el quince porciento" y luego al multiplicarlo por $12800$ obtenemos "el quince porciento de $12800$".

Un segundo pensamiento, para hacer más rápido aún todo, es que \(\frac{15}{100}\) es fácil de escribir como un número decimal: \(\frac{15}{100}=0,15\), ya que dividir por 100 es "correr" dos lugar a la izquierda la coma decimal, y esto nos lleva a la conclusión de que si, 0,15 es el 15%, 0,1 será el 10% porque \(\frac{10}{100}=0,1\) y 0,05 será el 5% porque \(\frac{5}{100}=0,05\) y así sucesivamente, lo que a su vez nos lleva a que:

Ventilete

Si un ventilador remueve aire, y por lo tanto lo vuelve "mas rápido"

1. ¿Por qué nos enfría en un día de verano?

2. ¿hay algún límite para que el efecto del ventilador funcione?

Pile-tongo

Aire a 24ºC, agua a 24ºC. Salimos del agua, y sentimos frío

1. ¿Por qué?

2. ¿Por qué no sentíamos frío estando fuera de la pileta?

¿Por qué cuando soplamos la sopa se enfría?

La temperatura de la sopa no es más que el promedio de la agitación de cada partícula de sopa. "Evaporarse" quiere decir, partículas saltando de la superficie de la sopa al aire, y las que primero saltan son las más agitadas. Por tanto, las que quedan en la sopa tienen una agitación media menor que antes: la sopa se ha enfriado.

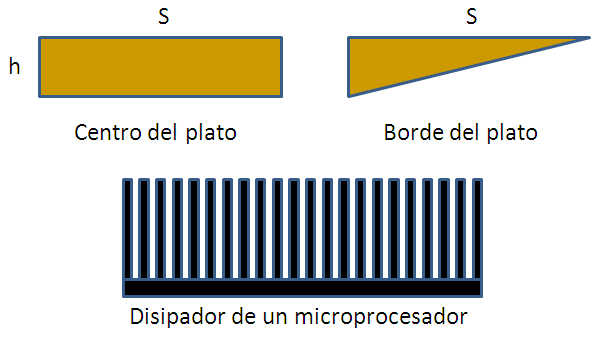
Ahora,

1. ¿Por qué cuando soplamos se enfría mas rápido?

2. ¿Qué parte del plato de sopa se enfría mas rápido? ¿Por que?

Lo que mata es la humedad

Proverbio de desmesurada porteñidad, reza que lo que el título que procede a este párrafo.

¿Por que nos sentimos mas incómodos en un día caluroso con clima húmedo respecto de otro igual de caluroso pero con clima seco?

Ma, alcanzame el toallón

Sabemos que la temperatura de ebullición del agua, es decir, a la cual toda el agua puede convertirse en vapor es de 100ºC. El agua caliente que usamos para bañarnos como mucho, tiene 40ºC ¿Por qué se forma vapor de agua si no se alcanza la tempertura de ebullición? ¿El agua "hierve" a menos temperatura en la ducha? ¿Como explicarías esto?

Repaso

Vimos previamente que una ecuación lineal de dos variables tenía como gráfico una línea recta, y que sus infinitos pares solución eran los que, cuando los ubicabamos en un par de ejes coordenados (o ejes de coordenadas o ejes cartesianos como prefieran llamarles) nos daban como dibujo una línea recta.

Una ecuación podría ser ésta:

Podemos, para facilitarnos el trabajo de "armar" la tabla de valores solución despejar una de las dos variables (o sea las letras $x$ e $y$ en este caso).

Voy a despejar la $y$:

Esto hace más facil saber "cuál es el valor de $y$ cuando hago que $x$ sea cierto valor", por ejemplo, supongamos que quiero saber cuánto debe ser $y$ cuando $x$ es $0$.

Por lo que el par \((0,-\frac{1}{2})\) es solución de la ecuación y por lo tanto, un punto del gráfico de nuestra recta. También lo es el punto \((1,1)\)

Una recta es algo que nunca se dobla, y aunque esto parece una estupidez no es así; como nunca se dobla todos los puntos que hacen una línea estan todos en fila uno atrás de otro, alineados. Vean que estoy diciendo cosas que parecen ser redundantes pero que su buena interpretación nos lleva esto:

Para gráficar correctamente una línea recta, sólo necesito conocer dos puntos que le pertenezcan

Uno marca los dos puntos (cada punto tiene un valor de $x$ y otro de $y$) en un par de ejes, y luego traza con regla o con imaginación, o con un software una línea que une esos dos puntos.

De las infinitas rectas que hay, existe sólo una que pasa por esos dos puntos, y es la que uno acaba de dibujar

Mira ahora el gráfico

¿Tiene sentido lo que estuve diciendo hasta ahora? Tratá de imaginar otra recta, diferente a la del gráfico y que También pase por los dos puntos que dije más arriba

La pendiente

Ahora, mirá este gráfico donde hay varias rectas:

¿Qué es lo que hace que algunas sean mas "empinadas" hacia arriba (si las miramos de izquierda a derecha, por ejemplo)? ¿Que hace que algunas apunten "para abajo"? ¿Por que algunas apuntan mas para arriba (o abajo) que otras?

Mirá el recuadro, ¿en qué se parecen y en que se diferencian estas ecuaciones?

1. \(y=3x\)

2. \(y=-x\)

3. \(y=\frac{1}{4}x\)

Ahora ¿en que se diferencian de esta otra?

1. \(y=\frac{3}{2}x+-\frac{1}{2}\)

Parámetros

Tenemos ahora el siguiente gráfico

Y el gráfico tiene un control que nos permite cambiar el número que multiplica a la $x$ desde $-10$ a $10$ ¿Qué cambia en la recta cuando damos a el parámetro $m$ diferentes valores?

Una pregunta que te podrás estar haciendo ahora, es ¿cuál es la diferencia entre dar valores a $x$ y obtener $y$ y lo que hacemos cuando usamos el control del gráfico de arriba?

Cuando lo que hacemos es encontrar los pares $(x, y)$ que satisfacen la ecuación, o sea, que forma una recta, estamos "averiguando" de que recta en particular se trata, digámoslo de otra manera: conocer los puntos de la recta, nos dice cual recta es de todas las que existen, en cambio, cuando cambiamos el parámetro de arriba, como verán, estamos alterando la recta ... estamos generando una nueva recta, que tendrá por lo tanto diferentes puntos solución, que, cuando los pongamos en un dibujo, serán los que forman la imagen que vemos en la pantalla.

Cada vez que tocamos el parámetro $a$ del gráfico de arriba, estamos creando una nueva recta que tendrá sus pares $(x,y)$, y que serán por lo tanto diferentes a los puntos de la anterior, porque estamos ante una recta diferente.

Ecuación genérica

¿Hay una forma de escribir una recta que sea a su vez "todas las rectas", una especie de recta "genérica"? Si, la hay, hay varias, y una es esta:

¿Cómo interpreto esta cosa?

Tenemos nuestras variables, $x$ e $y$, y luego dos letras, $m$ y $b$ que son parámetros. ¿Parámetros que hacen que cosa?

Bueno, en principio si decido dos números cualesquiera para $m$ y $b$, obtengo una recta en particular. Por ejemplo $m=2$ y $b=4$.

Así, eligiendo valores para $m$ y $b$ uno puede generar todas las rectas posibles del universo, mientras uno va pasando por todas las posibles combinaciones de números que se nos ocurran.

Juntando todo

Los parámetros que construyen las ecuaciones, nos permiten entender cómo están construidas las rectas y en qué se diferencian o parecen.

En la ecuación "genérica" el parámetro $m$ se le llama pendiente y al parámetro $b$ se le llama ordenada al origen o intersección con el eje vertical o término independiente.

Sin importar el nombre que usemos para los parámetros, podemos sumar una interpretación mas a todo el tema este de las ecuaciones de las rectas.

Lo relevante es entender e interpretar que rol juega cada parámetro mas allá de su nombre, y que cambia cuando uno los modifica.

• ¿Cómo es una recta con pendiente igual a cero?

• ¿Cómo debe ser una recta para que pase por el centro de coordenadas, es decir el punto $(0,0)$

• ¿Cómo influye el signo de la pendiente? ¿Y su valor absoluto? (es decir si es muy grande o muy chico sin importar el signo)

La interpretación

Esto nos dice entonces que para esta ecuación, sólo tenemos un posible valor par $x$, una vez que lo encontramos, no hay mucho mas que analizar. En términos textuales, hemos resuelto esto:

¿Cuál es el número que mupltiplicado por \(\frac{2}{3}\) nos da $6$?

En cambio ¿que pasa con la primera ecuación? Si elijo un valor para \(x`(digamos 0) obtengo una ecuación como la primera, donde puedo despejar $y$ y *hacer la cuenta* para obtener un valor para :math:`y\).

Esto, podríanos hacerlo para cualquier valor de \(x\) que quisiéramos y obtendriamos valores de \(y\) para cada uno de ellos.

La tabla

Si uno hace varias veces esto de elegir un valor para \(x\) y ver cuál es el de \(y\) que aparece (o al revés, escoge uno para $y$ para ver que $x$ nos da) y los ubica en una tabla obtiene algo como esto:

Esta tabla podría segur por siempre, es decir, podríamos usar cualquier número como valor de entrada y obtendríamos un infinitos pares asociados. Para cada $x$, hay una $y$.

Una ecuación lineal con dos varaibles, tiene infinitas soluciones son todos los pares $x$ e $y$ que cumplen con la igualdad (o sea los que obtenemos de despejar una de las dos variables y resolver)

El gráfico

Si ubicamos en un par de ejes perpendiculares (o sea, que forman 90 grados entre sí) los pares de valores \(x\) e \(y\) obtenemos esto:

Por convención, se usa el eje horizontal para la letra \(x\) y el vertical para \(y\). Tanto esto, cual es horizontal o cual vertical, y mismo el uso de las letras \(x\) e \(y\) es absolutamente arbirtario. Podríamos decir que:

A la comunidad matemática se le canto el quinto f***o del c**o usar estas letras y también decidió lo que le pintó para la ubicación de las letras en los ejes.

Esto quiere decir que, en realidad, no hay nada especial en los nombres y que uno podría usar cualquier letra y ubicar en el eje horizontal o vertical la que quisiera, siempre y cuando quede debidamente explicado en el gráfico.

Resumen

Juntando todo lo que acabamos de ver:

1. Una ecuación lineal tiene como solución infitos pares de valores

2. Esos pares de valores, graficados, forman una línea recta

Review

Last class topic was about how linear equations solutions can be thought as all points that creates a line. Whe have something like this:

or

And we can choose wathever value we like for one variable, and the other gets fixed and related. There is one $y$ value for each $x$ value, and vice-veresa, buth this pairs are unique.

Getting the line

If we plot linear equations solutions, we'll get lines. That's easy. But how can one identify which equation formed a given line?

Run and Rise

A way of telling which function (equation) belongs to a given plot it's to find $a$ and $b$. Fin $b$ it's straight because one has to look at $y$ axis interception. But ¿what about $a$?. A method is as follows:

1. Step on a point that belongs to the line (a solution, an $x$,$y$ pair)

2. Run to the right (left will be ok too, you'll se later) any given units you want (1,2,3)

3. Write down this value. We call it \(\Delta x\)

4. Rise (or go down) until you reach the line again

5. Count the units that took you there

6. Write down this value. We call it \(\Delta y\)

7. Do \(\frac{\Delta y}{\Delta x}\)

8. Result is $a$

Test what you've leanred

Excercises

Let's practice:

¿A que cosa llamamos calor? ¿Qué es la temperatura? ¿son lo mismo?

Buenos Aires, Resistencia o Gualeguaychú: Una enorme gota de sudor recorre la parte trasera de una nuca genérica, que espeta insultos específicos al viento, y que recuerdan lugares y propiedades de imposible existencia en el aire: "la recon... de este calor de m..".

Todos hemos experimentado esa horrible sensación de pesadez y fastidio. Lo sorprendente, es que un hecho tan cotidiano nos permita entender tantas cosas acerca del mundo y de yapa, contribuir a la división más famosa de la humanidad en dos: labandadelverano y labandadelinvierno (que de ahora en más, y en agradecimiento a esta genial nota , llamaremos LBDV y LBDI).

Wilsooooooooooooooooon

Para quien no haya visto la película Náufrago, ésta es un plagiodeplagiodeplagio de lo que le sucedió a Alexander Selkirk , un marinero escocés quien en 1703 fuera expulsado de su barco luego de discutir con el Capitán, y abandonado en una isla desierta a unos 650 kilómetros de Valparaíso (Chile) . Moraleja: si ud. es un marinero escoses en altamar, y es 1703, no le aconsejamos discutir con el capitán. O bueno, algo por el estilo.

Cinco años de soledad y su posterior rescate y vuelta a Gran Bretaña, además de hacer famoso a nuestro amigo Alexander, inspiró a William Defoe a escribir la novela Robinson Crusoe, que con múltiples variantes ha sido la "inspiración" de mucho otro material, como la película protagonizada por Tom Hanks que comenté hace un momento y también este poema de Borges:

Sueño que el mar, el mar aquel, me encierra

y del sueño me salvan las campanas

de Dios, que santifican las mañanas

de estos íntimos campos de Inglaterra.

Cinco años padecí mirando eternas

cosas de soledad y de infinito,

que ahora son esa historia que repito,

ya como una obsesión, en las tabernas.

Dios me ha devuelto al mundo de los hombres,

a espejos, puertas, números y nombres,

y ya no soy aquel que eternamente

miraba el mar y su profunda estepa

¿y cómo haré para que ese otro sepa

que estoy aquí, salvado, entre mi gente?

¿Que tiene que ver Selkirk con el calor? Bueno, que su método para generar fuego (hecho que le permitió sobrevivir) al frotar ramas de pimienta de Jamaica (no, no es la planta en la que están pensando) no podía ser explicado con el modelo del "calor" que existía hasta ese entonces.

Para las personas del 1700, lo que ocasionaba cambios de temperatura cuando dos objetos (cosas, entes, fluidos, gases, sólidos, vacas, cuñados y defensores de Banfield, bueno esto último no porque a esa fecha ni siquiera existía el fútbol) se ponían en contacto se explicaba de la siguiente manera:

Los cuerpos a mayor temperatura (que usualmente -pero no siempre- se sienten "mas cálidos" al tacto) tienen cierta cantidad de un fluido invisible (si, un fluido invisible ... un poco mejor que las ballenas que sostenían la tierra plana antigua) que al ponerse en contacto con otro a menor temperatura (osea con menos de este fluido) fluye libremente (del que tiene mas hacia el que tiene menos) para equilibrar los tantos, y ambos cuerpos acaban luego de un tiempo, con la misma cantidad de este fluido invisible (llamado calórico) y en consecuencia, a la misma temperatura.

Este modelo, el del calórico, explica mas o menos bien muchos fenómenos. Aunque no se lo veía, ni se lo podía medir: esto es una complicación pero no un argumento definitivo para desecharlo, de hecho nadie ha ido al sol y bien sabemos de que elementos esta compuesto. Sin embargo, ahora si viene la estocada: no podía explicar por qué al frotar dos cosas a la misma temperatura (osea con la misma cantidad de calórico) podíamos conseguir elevar aún mas la temperatura de ambos cuerpos ¿de donde salía este "calórico extra" ¿de las ballenas que sostienen la tierra? Blef.

Lo que había comenzado salvándole la vida a Selkirk, cuando pudo conseguir fuego al frotar sus ramitas, y que siguió cuando otros investigadores consiguieron calentar todo un objeto frotándolo contra si mismo, emitieron el certificado de defunción del calórico.

Entonces ...¿que es lo que provoca que algo aumente su temperatura?

Y sin embargo, se mueve

Cuentan (incomprobable) que Galileo Galilei, cuando fue enjuiciado por la inquisición cristiana debido a afirmar (entre otras blasfemidades de la época) que la tierra se movía, al momento de arrepentirse para ganarse así la ventaja de la prisión domiciliaria (y salvarse de potencialmente ser ejecutado) dijo por lo bajo: sin embargo se mueve, o en italiano: "Eppur si muove". Muestra cabal de que mas de uno es capaz de arrepentirse hasta de ser hijo de su propia madre, o sostener que la tierra no se mueve, con tal de que no lo ajusticien.

Galileo Moriría en 1642 encerrado en su casa de Pisa, antes de que existieran las mismas de muzzarella (que bien pueden pronunciarse "pisa" o "piza" o "pitza" o "picsa" según el paladar lingüístico de cada comensal, pero cuyo origen es, según los historiadores , la ciudad de Nápoles. Ja, alto dato). Ese año, nacía en las islas británicas, Isaac Newton (cuya biografía es menos apasionante que la de Galileo) y terminaría siendo quien sentaría las bases para entender, explicar y predecir el movimiento de todas las cosas del universo, desde los planetas, hasta el propio Galileo, o bueno, lo que quedara de él bajo tierra en ese entonces. La obsesión por explicar todos los fenómenos del mundo a través del movimiento, como un gran reloj, acaparó la visión del mundo de entonces.

Pero, discúlpeme señor, ¿No estábamos hablando de como las cosas se calientan y se enfrían? ¿Que tiene que ver el movimiento? ... y, algo debe tener que ver ¿no?

Veamos (o no): Algo que no podía hacer Newton entonces, y que fue objeto de discusión para la humanidad desde los griegos hasta fines del siglo XIX y principios del siglo XX era observar directamente la estructura de la materia con "zoom infinito" para ver como estaba compuesta. Ciertos científicos, postulaban que, si uno pudiera ir "rompiendo" la materia en partes cada vez mas pequeñas, llega un momento en que uno se topa con algo que no se puede dividir en partes. Algunos griegos, como Demócrito y Leucipo eran partidarios de esto, y llamaron a esas unidades, átomos (osea a-tomos, osea que no tiene partes o tomos) confiriéndoles el papel de ser los "ladrillos del universo".

Fue así que, ya con el calórico fuera de combate, muchos científicos empezaron a suponer que, eran estos ladrillos o partículas los que al moverse (gracia'newton) de manera caótica y chocar entre sí, producían la elevación de la temperatura de los cuerpos. Cuanto mas movimiento se le da a las partículas de un objeto, más caliente se vuelve. Todas las cosas, desde las sólidas a los gases, pasando por los fluidos están hechos de estas partículas, que se mueven constantemente, vibran, como una muchedumbre de pie en un estadio, uno junto a otro, empujándose entre todos. Cuanto mas grande la vibración de estas partículas mas se irá calentando ¿Hay un límite para esto?¿Es igual en todas las sustancias?¿absolutamente todas las partículas aumentan o disminuyen por igual su movimiento?¿de que depende? ¿pueden nuestras partículas ayudar a explicar los diferentes estados de la materia?Muchas preguntas por ahora, pero hagamos un alto, y volvamos al tema central, la relación entre temperatura y movimiento.

Moving, just keep moving

Ahora tenemos un nuevo modelo: el modelo cinético de partículas (pa vos, calórico, gil) que nos permitiría explicar algunos fenómenos térmicos, veamos que nos ofrece.

Pongo dos cuerpos en contacto, uno esta a una temperatura $T_1$ y el otro a una temperatura mayor, $T_2$. ¿Que debería suceder? Las partículas mas agitadas del cuerpo a $T_2$ irán chocando entre sí y a su vez con las del cuerpo a $T_1$, en ese intercambio, las partículas del cuerpo a $T_2$ ser irán ralentizando y las de $T_1$ moverán mas rápido que antes. A ese flujo de energía producto de una diferencia de temperaturas, es a lo que los científicos llaman calor. Así lo que observaríamos es que el cuerpo a $T_2$ debería disminuir su temperatura, y el cuerpo a $T_1$ aumentarla. Por supuesto que la magnitud de este "equilibramiento" depende de las cantidades de cada cuerpo, por ejemplo: Si mezclo 1000 litros de agua a 100ºC con 1 litro de agua a 30ºC, sin ser ningún genio, uno puede suponer que el efecto de "ralentizarse" de las partículas del cuerpo que está a 100ºC será mucho menor que el efecto de "volverse mas rápidas" que experimentan las partículas del cuerpo a 30ºC, y acabaremos con una mezcla de agua, mucho mas cerca de 100ºC (menos que 100ºC) que de 30ºC. punto para el modelo de partículas, esto es justamente lo que pasa.

No tengo idea, peeero...

Como vimos en esta clase, la ciencia ofrece explicaciones para lo que suecede o sucederá en nuestra realidad, y cuando las ideas o modelos que se usan encuentran limitaciones o no son capaces de explicar algunos hechos, o peor aún, predicen cosas que contradicen a las que suceden, los modelos deben ser modificados o abandonados por otros que permitan explicar cada vez más cantidad de fenómenos y por supuesto, aquellos que antes no.

La idea de que todo está hecho de pequeñas partículas, es bastante interesante, pero, como resulta evidente, se trata de objetos no podemos observar, por lo que, de momento no nos interesa saber si efectivamente existen, sino sólo suponer que existen y seguir el razonamiento: Si todo está hecho de pequeñas partículas, y estas partículas pueden moverse y desplazarse (mas o menos), vibrar o rotar, entonces ... y luego del entonces podremos completar con cosas que intentemos explicar y ver si efectivamente están de acuerdo con nuestra idea.